Abstract
The nonlinear behavior of a sinusoidally modulated rotating disk electrode (RDE) is analyzed to identify the flow and concentration field interactions
that lead to resonance and nullification conditions in the electrochemical response of the system. Steady periodic solutions to the von Kármán self-similar
form of the Navier–Stokes equations and convective diffusion equation are examined using a combined Fourier transform/perturbation approach that yields a
set of frequency dispersion equations solved using the finite element method. Experimental measurements using a RDE with sinusoidal angular velocity
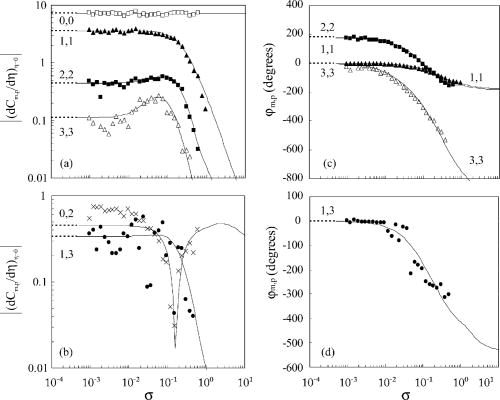
waveform Ω=Ω0+ΔΩcos(ω0t) are compared to theory for modulation amplitudes ΔΩ∕Ω0<1 and electrolyte Schmidt number of 1680.
The modulation frequency ω0 is varied from the quasisteady to high-frequency limits to obtain the phase and amplitude
of the mean, fundamental, and higher-harmonic limiting current. We show that distinct features (resonances and nullifications) in the nonlinear mean
and higher harmonic components of limiting current result from constructive and destructive (in phase and 180° out of phase, respectively) interactions
between cross terms of the oscillating components in the axial flow and concentration fields near the disk surface.
# Graphical Abstract